If you’d like to drop in for a visit, my desk is S33°56’41” and E18°25’41”. Peering at these numbers on my phone, I swear I can hear generations of sextant-clutching land surveyors weeping. The device has done to them what the motorcar did to wheelwrights and farriers.

It got me wondering, though, what I was 33° south of and 18° east of — and who figured it all out. Some digging led me to a story about a well in Syene (now drowned by the Nile’s High Aswan Dam) and a brilliant Greek librarian and mathematician with the grand name of Eratosthenes.

The year was around 200BC, the date 21 June. On noon that day, the sun shone straight down the deep well, leaving no shadows. Nothing so strange had ever been seen in the Egyptian city of Alexandria where Eratosthenes lived.

In those days, it was generally accepted that the Earth was flat and that the moon, sun and stars were fixed to the underside of a celestial sphere which rotated round the motionless Earth. Who, indeed, could say they had felt the Earth move?

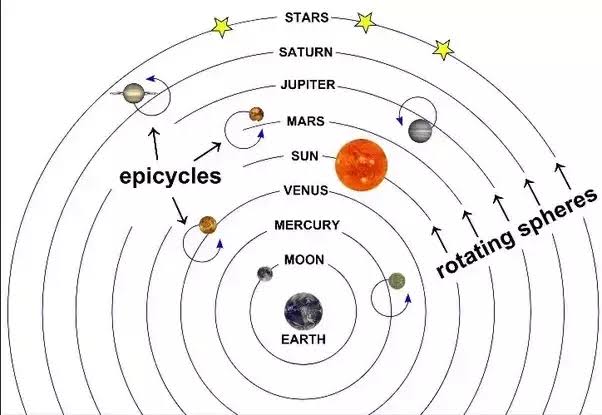
Prolemy’s solar system (Image WikiCommons)

The Greeks knew, however, that the sun inexplicably migrated north in summer and south in winter. They named the extremes of this migration “tropics”, after the word tropos meaning turn. The midpoint between the turns they termed “equator”.

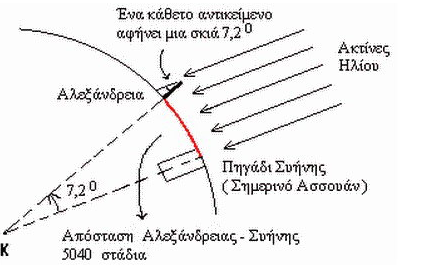
Eratosthenes was fascinated by the story of the well, which a traveller had told him. It meant that at that time and place, the sun was directly overhead, on what we know today as the Tropic of Cancer. But he had another idea: Maybe the Earth was round and somehow wobbled. After all, Socrates had noticed that ships sailing out to sea disappeared hull first and had suggested the possibility that the Earth was on a celestial ball.

(Image WikiCommons)

If the sun’s rays were parallel and the Earth was a sphere, thought Eratosthenes, sunlight would hit different parts of the Earth’s surface at different angles. If he could discover the distance between Syene and Alexandria, then measure the angle of the shadow on the same midsummer day in Alexandria, he could use the triangle theorem of another Greek, Pythagoras, to measure the size of the Earth.

Travellers gave him the rough distance between the well and his library in Alexandria, and the shadow gave him two sides of a triangle. He found the angle between the top of his pole and the tip of its shadow to be about one fiftieth of a circle, so he simply multiplied the distance between Syene and Alexandria by 50 and declared the circumference of the Earth to be 46,250km. He was only 6,000km out – and one must remember this was around 200BC.

Eratosthenes is rightly considered the father of modern cartography, the science of mapmaking.

Eratosthenes (Image WikiCommons)

For about 400 years, this information lay in the great library of Alexandria, awaiting another genius who could comprehend its implications. That person was Claudius Ptolemy. His interests ran from biography and music to mathematics and optics, but his influence has come down through the centuries from two monumental books, one on astronomy and the other on geography.

Prolemy (Image WikiCommons)

He got many things wrong – it was 200AD after all – but what he gave to the world is the subdivision of the degrees of a circle into minutes and seconds, and the notion that maps should be drawn with reference to these subdivisions as measurable coordinates. The task of the cartographer, he said, was to “survey the whole in its just proportions.”

There is a parallel claim to this notion. The Chinese cartographer Chang Heng – a near contemporary of Ptolemy – wrote that a cartographer’s job was to “cast a network of coordinates about heaven and Earth, and reckon on the basis of it”.

The source of his inspiration, it seems, came from a girl who was employed to embroider one of Chang’s maps on silk. When he saw the intersecting lines of warp and weft, he was struck by their net-like effect on his map.

Eratosthenes had established three lines of longitude: the equator and the tropics of Cancer and Capricorn (named after star signs which coincided with summer and winter equinoxes). Ptolemy divided the circle of the planet as viewed from one of the poles into degrees, each of which was a line of longitude. It was he who originated the practice of placing north at the top, simply because most of the known world at the time was in the northern hemisphere and maps were easier to study with the land on top and all the writing and fanciful sketches below.

In the 500-year-old library of Alexandria, where both men had laboured, lay all the basic tools of modern cartography for the mapping of the planet. Then disaster struck. In the year 391, zealots sacked the library of Alexandria and burned its priceless contents, a symbolic victory of faith over reason.

Library of Alexandria (Image WikiCommons)

We today cannot know what knowledge the world lost that day. Some works were hastily smuggled out, but most went up in flames, including much of the formulations of Eratosthenes and Ptolemy. Cartography was dealt a deadly blow. The Earth, once again, became flat, the sun and stars were reattached to their ever-circling heavenly sphere and science died.

During the thousand-year slough of intellectual stagnation which followed – named the Dark Ages for good reason – surviving copies of the ancient cartographic texts were hidden by scholars and monks, and handed down in secrecy. Maps reverted to being wildly speculative – more ecclesiastical than cartographic – and mostly dead wrong.

They sported the demons of the time: horse-footed men with ears so long, they covered their bodies, savages who quaffed mead from human skulls, griffons with savage beaks, pythons which grew fat on the udders of cows, a cockatrice with crocodile forequarters and hindquarters suspended from lateral fins. It was thought that at the equator, the seas would boil a boat to pieces.

The Renaissance and brave Portuguese mariners would change all that, dragging a slumbering Europe into a confrontation with the ideas of Greece’s Golden Age and the exotic wonders of a New World.

Early in the 15th century, Ferdinand Magellan circumnavigated the planet and it could never again be flat. The Portuguese drew maps; not good ones, but with usable information for adventurers to follow. And follow they did.

During the next century, Eratosthenes’s triangulation was dusted off and reinstated in the universities of Lisbon, Ptolemy’s notion of grids and degrees was widely debated in the salons and shipping offices of the great ports of Europe.

But the problem of how to fix a point on the Earth remained elusive. By what method could you know exactly how far you were from the equator, the pole or the nearest shore? Sailors died in the absence of this information. Explorers became hopelessly lost. The problem was that since the size of the Earth was not known, the exact distance that a degree of latitude or longitude covered at any point was mere guesswork.

Enter Jean Picard. In 1669, this Frenchman – laboriously laying end on end well-seasoned, varnished wooden rods – measured an 11.4km baseline from Paris to Fontainebleau. Then, by Pythagorian triangulation, he sighted an arc from Paris to a clock tower in the village of Sourdon. Several other triangulations later, he calculated – I will not tax you with his mathematics – that a degree of latitude measured 110.46km, a remarkably accurate result.

Jean Picard (Image WikiCommons)

There was, however, a problem. Picard’s measurement would be fine if the Earth was a perfect sphere. But was it? Isaac Newton in England suggested that, because of centrifugal force, the Earth bulged at the equator and flattened at the poles. The French Royal Academy of Sciences, for some reason, thought it was flatter round its waist and pointy at the poles.

To solve the problem, the academy laid plans for two geodetic expeditions, one to Peru on the equator, the other to the Arctic Circle. They were to be terrible trips.

In 1736, French Academy member Pierre Louis Moreau de Maupertuis set off for Lapland with three other academy members, a priest and a good deal of equipment.

Maupertuis in Finland (Image WikiCommons)

The Swedish king tried to dissuade them from “so desperate an undertaking”. But the party pressed on to the icy northern end of the Gulf of Bothnia where they made a base. Then they proceeded up the Torne River, braving cataracts and “flies with green heads that fetch blood wherever they fix”.

Lapland was almost a picnic compared to Peru. The other expedition, led by Pierre Bouguer and Charles Marie de La Condamine, encountered (as Bouguer wrote) “difficulties not to be imagined”. The Peruvians and Spanish were suspicious: Who could believe the ridiculous story about measuring arcs and fixing meridians?

Using methods pioneered by long-dead Eratosthenes, they triangulated their way across the Arctic Circle, laying base lines with chains and taking sightings on mountain peaks and known stars. To get accurate fixes, they would climb peaks, strip the bark off trees to make them more visible and build log pyramids. The effort amid the snow and ice was unthinkable. Fog and a forest fire they had started by accident delayed them.

After nearly two months of sightings, they headed south, winter freezing the river behind them as they travelled. When it was all over, Maupertuis made his calculations. A degree, he found, was 111.094km, more than half a kilometre difference between a degree measured in France. The Earth was definitely not a perfect sphere.

Lapland was almost a picnic compared to Peru. The other expedition, led by Pierre Bouguer and Charles Marie de La Condamine, encountered (as Bouguer wrote) “difficulties not to be imagined”. The Peruvians and Spanish were suspicious: Who could believe the ridiculous story about measuring arcs and fixing meridians?

His calculations showed that a degree of latitude at the equator was 109.92km, shorter than in Europe. The Earth was definitely more curved at the equator and flatter at the Arctic Circle.

The party persevered amid hostilities, triangulating from Quito near the equator to a place named Cuenca in the Andes Mountains. Every angle measured was a testament to their endurance.

They hacked their way up the Andes, where members fainted from the altitude and had “little haemorrhages” of the lungs. Clouds prevented sightings, rain fell for weeks on end. They lived on bad cheese and biscuits made from hard maize. One of the party, a surgeon, was killed in an argument in a village; a botanist suffered a mental breakdown and never recovered. The expedition took nine-and-a-half years. La Codamine became the first foreigner to raft down the Amazon River.

His calculations showed that a degree of latitude at the equator was 109.92km, shorter than in Europe. The Earth was definitely more curved at the equator and flatter at the Arctic Circle.

Given that the Arctic party had returned many years earlier, La Codamine arrived in Paris with incredible tales of the Andes and Amazon, but no startling news. His weary lament: “We returned seven years too late to inform Europe of anything new concerning the figure of the Earth.”

In order to fix the imaginary planetary grid in place only, one line remained to be settled. The equator is where it is because that position is halfway between the poles. It is the line of zero latitude, the prime parallel, and it could run nowhere else. But the line of zero longitude, the prime meridian, is another matter. It is arbitrarily designated and could be almost anywhere – and at one time or another, it has been.

Ptolemy chose the Fortunate Islands, the westernmost extremity of his known world. Depending on the origin of the map, it has also run through Toledo, Cadiz, Madrid, Cracow, Copenhagen, Pisa, Naples, Rome, Augsburg, Ulm, Tubingen, Peking, St Petersburg, Washington, Philadelphia and Greenwich.

This caused immense confusion when pinpointing coordinates on maps so, in 1884, the US government called an International Meridian Conference. At that meeting, with few dissenting votes, the Royal Observatory at Greenwich was chosen to be zero longitude. The grid was complete.

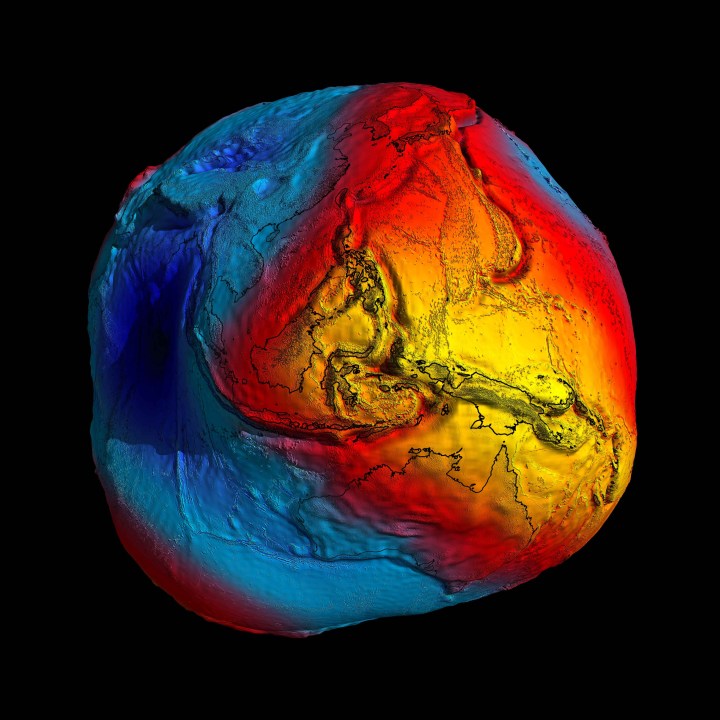
There is a sequel to this story which has to do with the cellphone in my hand. Satellites in space are now used as points for geodetic triangulation. Their use in global positioning systems makes cartographic calculations mind-bogglingly accurate. It has been confirmed that the Earth is flattened, but not by much. Its equatorial diameter exceeds the polar diameter by a mere 42.77km.

Triangulation (Image WikiCommons)

But GPS accuracy has turned up something even more surprising, which would have got those old surveyors with their rods and chains really excited. It is also strangely charming.

Using instruments capable of measuring distances to within a couple of centimetres, plus dozens of satellites and more than half a million optical, radio and laser sightings, the US Goddard Space Flight Centre recently found that the southern hemisphere is larger than the northern hemisphere.

The Earth is ever so slightly pear-shaped. DM/ML