EDUCATION CHALLENGES
See the ‘unsolvable’ problem in the matric maths paper and an expert’s possible solution
Students at Menlopark High School begin the annual National Senior Certificate Examination or Matric Final Examination on 31 October 2022 in Pretoria, South Africa. (Photo: Gallo Images / Beeld / Deaan Vivier)
An alleged error in a trigonometry question in the Grade 12 Mathematics Paper 2 has caused an uproar among learners and teachers. The Department of Basic Education is investigating. While we wait, an expert here explains the problem, and also what it would take to make the question solvable.
The maths problem in question is as follows:
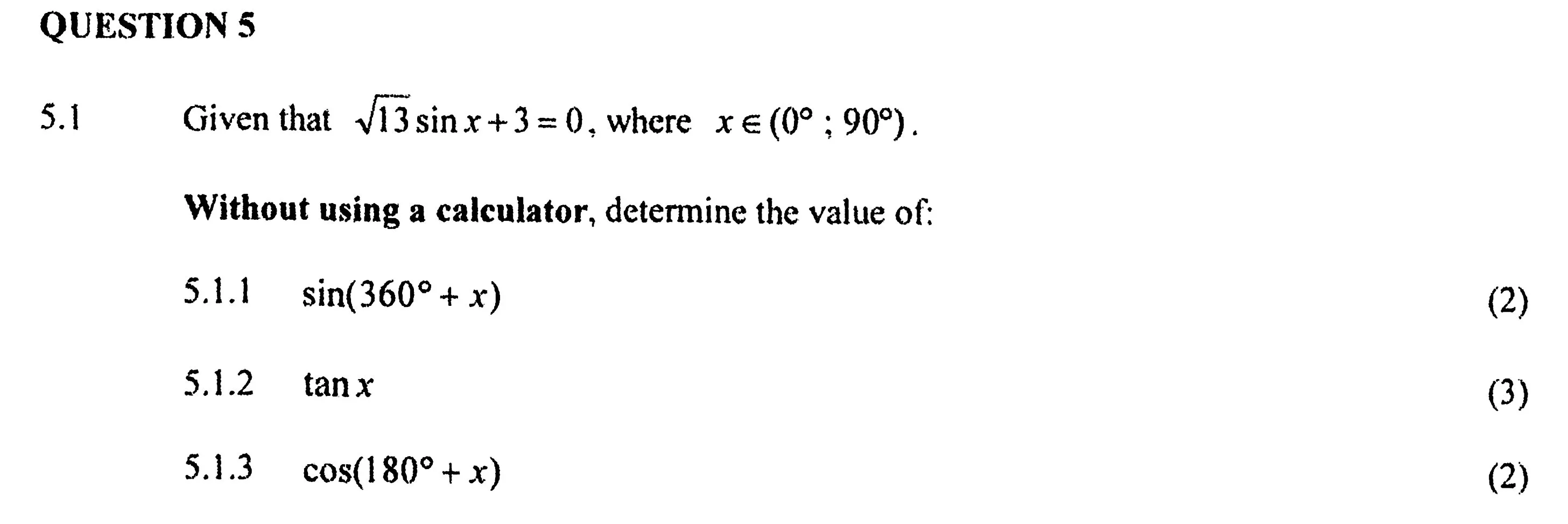
The ‘impossible’ seven-mark question in the matric maths exam paper.
Nicky Roberts, a professor of mathematics education at the University of Fort Hare and director of Kelello Consulting, concluded that the question is impossible to solve. She explained it as follows, and resolved that the only way to solve the problem would be to amend the question.
Read more in Daily Maverick: “Solving the unsolvable 5.1 problem — disastrous matric maths question stumps teachers and learners alike”
Sums of all fears: The seven steps I used to help my kids survive matric
Become an Insider
Could we square Both sides of equation Sinx=-3/sq root of 13 (could we do this.)
Thus (sinx)sq=9/13
Take sq root on both sides and Sinx=+or – 3/sq rt of 13
Using Pythagoras the side adjacent to angle x is now 2, opposite side is 3 and hypotenuse=Sq rt 13
Thus Tan x=-3/2
Sin(360+x)=-3/sq rt 13
Cos(180+x)=2/sq rt of 13
Actually there is a solution (though even experts can be forgiven for not spotting a diabolical point), as 13 has TWO roots, one positive and one negative.
The negative root is -3.6056 (-3.6056 × -3.6056 = 13).
As we are given that x is in the first quadrant, sin x must be positive (as pointed out), and that can be achieved if one uses the negative root of 13.
If this was the intended solution – I agree that the suggested error with the sign is more likely – then this is way too sneaky for a matric paper. More like a Maths Olympiad problem, and one that would even then bamboozle many of the better mathematicians in the country.
So then the question, although bamboozling, can be answered. That being the case it should stand and only the best of the best young mathematicians might achieve the 7 marks available.
When a root is given in a problem, as it is here, the root is only the positive or only the negative root. In this case since there is no negative symbol in front of the sqrt(13) it can be interpreted only as the positive square root of 13.
If a student solves a problem by square rooting a number then they are required to consider both possibilities. i.e. x^2 = 4 then x = +/- 2.
I said the same but then a maths professor (and the guide to the US SAT maths) said that when using that SQRT symbol it is always the positive. If they had said K x sin(X) + 3 = 0 where k^2=13 and stuck to saying X is 0-90 degrees our logic would hold and without need for calculator as one only use k^2 to solve the questions, not k. I’d have given bonus marks to kids that set out their approach and reason and gave the logical answers
Technically the square root of 13 has a positive and a negative value. But matric maths students are always taught to take the positive root by default. I am not sure why. Perhaps the examiner wanted to make the point that square roots can be + or – . Not really fair on matric students who should be automatically awarded all the marks on this question. And the examiner can then go and have his/her ‘boxing match’ over the status quo – ie always take positive root.
I’m with Hartmut, and whatever he says!
Great that you’re rooting for Hartmut! (in the positive I take it 😀 )
A big fuss about nothing as it is just a difficult problem to solve for most Grade 12.
The root of all problems is the ANC. It is always negative.
Agreed 100%. Lets add that the ANC can only add a negative value to any problem or solution. Whether it is square root, root beer, uproot working SOE’s a negative vale is expected in an ANC execution of a winning plan.
But you only need to be 30% correct!
Prof Roberts is correct – both of the given conditions cannot be true at the same time. The arguments for using the negative square root of 13 are irrelevant, because this number represents the hypotenuse/radius of the circle in which angle x falls, and this value cannot be negative for any angle in the Cartesian Plane. Only the opposite (y-value) and the adjacent (x-value) sides of the triangle can be either negative or positive, depending on which quadrant the angle is in.
As stated by Prof Roberts, if the angle is in the first quadrant, the equation can only be solved if +3 is replaced with -3. If the equation is to stand, then the angle must be in the third or fourth quadrant, not in the first as given in the exam paper.
I don’t think it was meant to be ‘diabolical/sneaky/bamboozling/Olympiad-level’ at all, probably just sloppy proof-reading. If the proof-reader/external moderator had simply tried to solve the problem, it likely would have been picked up.
I think the fairest outcome would be to award full marks for that question to everyone, although that doesn’t compensate for the time lost trying to figure it out. Re-writing a whole new whole paper could affect maybe thousands of youngsters who had other commitments.
The equation involves a trigonometric function which can be mapped to the properties of a triangle, but just because a constant is in front of the sin(x) that does not make the constant a radius or a hypotenuse. It is just a number multiplying the term. If it had been written as -3.605 sin(x) + 3 = 0 then it would have been solved without great difficulty and with no talk of negative radii (albeit needing a calculator!).
Agreed, solving for sin(x) would be simple with a calculator, and sin(360+x) is then the same as sin(x). They would also need a calculator to answer the tan and cos questions, and might have to figure out whether to use the negative or positive root. But without a calculator, and given that the questions relate to trigonometric ratios, it’s hard to imagine how else they might do this without relying on Pythagorus. One would assume they were taught to draw a rough figure and fill in the opposite, adjacent and hypotenuse values.
I’m keen to see how the Department eventually rules on this one! Hopefully the DM will keep us posted.
The purpose of an examination is to establish what the examinee knows rather than what they dont. If that is the underlying purpose, how does this question assist the examiner? For 7 marks it seems inappropriate?
Pretty obvious error which any matriculant should pick up immediately.
State impossible since sinx for x between ) 0 and 90 is positive and collect full marks for the question so get your 7 marks very quickly and gain time